IUPAC-NIST Solubility Database
NIST Standard Reference Database 106
 Introduction:
Introduction:
Web Version 1.0
A database containing solubilities originally published in the IUPAC (International Union for Pure and Applied Chemistry) - NIST Solubility Data Series is now available online.
Mutual solubilities and liquid-liquid equilibria of binary, ternary and quaternary systems are presented. Typical solvents and solutes include water, sea water, heavy water, inorganic compounds, and a variety of organic compounds such as hydrocarbons, halogenated hydrocarbons, alcohols, acids, esters and nitrogen compounds. For many systems, sufficient data were available to allow critical evaluation. Data are expressed as mass and mole fractions as well as the originally reported units.
Scope: There are over 67,500 solubility measurements, compiled from 18 volumes of the IUPAC Solubility Data Series.
There are about 1800 chemical substances in the database and 5200 systems, of which 473 have been critically evaluated. The database has over 1800 references.
Updated: March, 2006
IUPAC-NIST Solubility Data Series
V.P. Sazonov and D.G. Shaw
1. Introduction to the Solubility Data Series
1.1 The Nature of the Project
The Solubility Data Project (SDP)
has as its aim a comprehensive review of published data for solubilities of
gases, liquids and solids in liquids or solids. Data of suitable precision are
compiled for each publication on data sheets in a uniform format. The data for
each system are evaluated and, where data from different sources agree
sufficiently, recommended values are proposed. The evaluation sheets,
recommended values, and compiled data sheets are published on consecutive pages.
This series is concerned primarily
with liquid-liquid systems, but a limited number or related solid-liquid,
fluid-fluid and multi-component (organic-water-salt) systems are included where
it is considered logical and appropriate. Solubilities at elevated and low
temperatures and at elevated pressures have also been included, as it is
considered inappropriate to establish artificial limits on the data presented if
they are considered relevant or useful.
For some systems, the two components may be miscible in all proportions at certain temperatures and
pressures. Data on reported miscibility gaps and upper and lower critical
solution temperatures are included where appropriate and when available.
1.2. Compilations and
Evaluations
The formats for the compilations and critical evaluations have been standardized for all
volumes. A description of these formats follows.
1.3. Compilations
The format used for the compilations is, for the most part, self-explanatory. A compilation sheet is
divided into boxes, with detailed contents described below.
Components: Each component is listed according to
IUPAC name, formula, and Chemical Abstracts (CA) Registry Number. The Chemical
Abstracts name is also included if this differs from the IUPAC name, as are
trivial names if appropriate. IUPAC and common names are cross-referenced to
Chemical Abstracts names in the System Index. The formula is given either in
terms of the IUPAC or Hill1 system and the choice of
formula is governed by what is usual for most current users: i.e., IUPAC for
inorganic compounds, and Hill system for organic compounds. Components are
ordered on a given compilation sheet according to:
- saturating components;
- non-saturating components in alphanumerical order;
- solvents in alphanumerical order.
The saturating components are arranged in order according to the IUPAC 18-column periodic table with two
additional rows: Columns 1 and 2: H, alkali elements, ammonium, alkaline earth
elements;
- Columns 3 to 12: transition elements;
- Columns 13 to 17: boron, carbon, nitrogen groups; chalcogenides,
halogens;
- Column 18: noble gases;
- Row 1: Ce to Lu;
- Row 2: Th to the end of the known elements, in order of atomic number.
Organic compounds within each Hill
formula are ordered in the following succession:
- by degree of unsaturation;
- by order of increasing chain length in the parent hydrocarbon;
- by order of increasing chain length of hydrocarbon branches;
- numerically by position of unsaturation;
- numerically by position by substitution;
- alphabetically by IUPAC name.
Example:
| C5H8 |
cyclopentane |
| |
2-methyl-1,3-butadiene |
| |
1,4-pentadiene |
| |
1-pentyne |
| C5H10 |
cyclopentane |
| |
3-methyl-1-butene |
| |
2-methyl-2-butene |
| |
1-pentene |
| |
2-pentene |
| C5H12 |
2,2-dimethylpropane |
| |
2-methylbutane |
| |
pentane |
| C5H12O |
2,2-dimethyl-1-propanol |
| |
2-methyl-1-butanol |
| |
2-methyl-2-butanol |
| |
3-methyl-1-butanol |
| |
3-methyl-2-butanol |
| |
1-pentanol |
| |
2-pentanol |
| |
3-pentanol |
| C6H12O |
cyclohexanol |
| |
4-methyl-1-penten-3-ol |
| |
1-hexen-3-ol |
| |
4-hexen-3-ol |
Deuterated (2H) compounds follow immediately the corresponding H
compounds.
Original Measurements: References are
abbreviated in the forms given by Chemical Abstracts Service Source Index
(CASSI). Names originally in other than Roman alphabets are given as
transliterated by Chemical Abstracts. In the case of multiple entries (for
example, translations) an asterisk indicates the publication used for
compilation of the data.
Variables: Ranges of temperature, pressure, etc. are
indicated here.
Prepared by: The names of all compilers are given here.
Experimental Values: Components are described
as (1), (2), etc., as defined in the "Components" box. Data are reported in the
units used in the original publication, with the exception that modern names for
units and quantities are used; e.g., mass per cent for weight per cent; mol
dm–3 for molar; etc. In most cases, both mass and molar values are
given. Usually, only one type of value (e.g., mass per cent) is found in the
original paper, and the compiler has added the other type of value (e.g., mole
per cent) from computer calculations based on 1989 atomic weights2. Temperatures are expressed
as t/°C, t/°F or T/K as in the original; if necessary,
conversions to T/K are made, sometimes in the compilations, and always in
the critical evaluation. However, the author's units are expressed according to
IUPAC recommendations3
as far as possible.
Errors in calculations, fitting
equations, etc. are noted, and where possible corrected. Material inserted by
the compiler is identified by the word "compiler" or by the compiler's name in
parentheses or in a footnote. In addition, compiler-calculated values of mole or
mass fractions are included if the original data do not use these units. If
densities are reported in the original paper, conversions from this is done in
the evaluation, with the values and sources of the densities concentrations to
mole fractions are included, but otherwise being quoted and referenced.
Details of smoothing equations (with limits) are included if they are present
in the original publication and if the temperature or pressure ranges are wide
enough to justify this procedure and if the compiler finds that the equations
are consistent with the data.
The precision of the original data is preserved when derived quantities are
calculated, if necessary by the inclusion of one additional significant figure.
In some cases graphs have been included, either to illustrate presented data
more clearly, or if this is the only information in the original. Full grids are
not usually inserted as it is not intended that users should read data from the
graphs.
NOTE: The fields BestSolExp, x1Exp, and x2Exp indicate, for example, a solubility value of 6.8 with a Exp of -3 means 6.8E-3. Similarly, SolPower, BestSolPower, x1Power, and x2Power, means, for example, a solubility value of 4.6 with a Power of -4 means 4.6E-4. In addition, a solubility value of 9.47 with Sol. Power of 2 and a Solx10(**) of -4 means a solubility of 9.47 100 g/g times 1E-4 or 9.47E-6. These notations reflect that provided by the evaluator.
Method: The apparatus and procedure are mentioned
briefly. Abbreviations used in Chemical Abstracts are often used here to save
space, reference being made to sources of further detail if these are cited in
the original paper.
Source and Purity of Materials: For each component,
referred to as (1), (2), etc., the following information (in this order and in
abbreviated form) is provided if available in the original paper: source and
specified method of preparation; properties; degree of purity.
Estimated Errors: If estimated errors were omitted
by the original authors, and if relevant information is available, the compilers
have attempted to estimate errors (identified by "compiler" or the compiler's
name in parentheses or in a footnote) from the internal consistency of data and
type of apparatus used. Methods used by the compilers for estimating and
reporting errors are based on Ku and Eisenhart4.
Comments and/or Additional Data: Many
compilations include this section which provides short comments relevant to the
general nature of the work or additional experimental and thermodynamic data
which are judged by the compiler to be of value to the reader.
References: The format for these follows the
format for the Original Measurements box, except that final page numbers are
omitted. References (usually cited in the original paper) are given where
relevant to interpretation of the compiled data, or where cross-reference can be
made to other compilations.
1.4. Evaluations
The evaluator's task is to assess the reliability and quality of the data, to
estimate errors where necessary, and to recommend "best" values. The evaluation
takes the form of a summary in which all the data supplied by the compiler have
been critically reviewed. There are only three boxes on a typical evaluation
sheet, and these are described below.
Components: The format is the same as on the Compilation sheets.
Evaluator: The name and affiliation of
the evaluator(s) and date up to which the literature was checked.
Critical Evaluation:
(a) Critical text. The evaluator checks that the compiled data are correct, assesses their
reliability and quality, estimates errors where necessary, and recommends
numerical values based on all the published data (including theses, reports and
patents) for each given system. Thus, the evaluator reviews the merits or
shortcomings of the various data. Only published data are considered. Documented
rejection of some published data may occur at this stage, and the corresponding
compilations may be removed.
The solubility of comparatively few systems is known with sufficient accuracy
to enable a set of recommended values to be presented. Although many systems
have been studied by at least two workers, the range of temperatures is often
sufficiently different to make meaningful comparison impossible.
Occasionally, it is not clear why two groups of workers obtained very
different but internally consistent sets of results at the same temperature,
although both sets of results were obtained by reliable methods. In such cases,
a definitive assessment may not be possible. In some cases, two or more sets of
data have been classified as tentative even though the sets are mutually
inconsistent.
(b) Fitting equations. If the use of a smoothing equation is justifiable the
evaluator may provide an equation representing the solubility as a function of
the variables reported on all the compilation sheets, stating the limits within
which it should be used.
(c) Graphical summary. In addition to (b) above, graphical summaries are
often given.
(d) Recommended values. Data are recommended if the results of at least two
independent groups are available and they are in good agreement, and if the
evaluator has no doubt as to the adequacy and reliability of the applied
experimental and computational procedures. Data are reported as tentative if
only one set of measurements is available, or if the evaluator considers some
aspect of the computational or experimental method as mildly undesirable but
estimates that it should cause only minor errors. Data are considered as
doubtful if the evaluator considers some aspect of the computational or
experimental method as undesirable but still considers the data to have some
value where the order of magnitude of the solubility is needed. Data determined
by an inadequate method or under ill-defined conditions are rejected. However,
references to these data are included in the evaluation together with a comment
by the evaluator as to the reason for their rejection.
(e) References. All pertinent references are given
here, including all those publications appearing in the accompanying compilation
sheets and those which, by virtue of their poor precision, have been rejected
and not compiled.
(f) Units. While the original data may be reported in the units used by the
investigators, the final recommended values are reported in SI units3 when the data can be
converted accurately.
1.5. Quantities and Units Used in Compilation and Evaluation of
Solubility Data
1.5.1. Mixtures, Solutions and Solubilities
A mixture5,6
describes a gaseous, liquid or solid phase containing more than one substance,
where the substances are all treated in the same way.
A solution5,6 describes a liquid or solid phase containing more than one substance, when for
convenience one of the substances, which is called the solvent, and may
itself be a mixture, is treated differently than the other substances, which are
called solutes. If the sum of the mole fractions of the solutes is small
compared to unity, the solution is called a dilute solution.
The solubility of a solute 1 (solid, liquid or gas) is the analytical
composition of a saturated solution, expressed in terms of the proportion of the
designated solute in a designated solvent7.
"Saturated" implies equilibrium with respect to the processes of dissolution
and demixing; the equilibrium may be stable or metastable. The solubility of a
substance in metastable equilibrium is usually greater than that of the same
substance in stable equilibrium.(Strictly speaking, it is the activity of the
substance in metastable equilibrium that is greater.) Care must be taken to
distinguish true metastability from supersaturation, where equilibrium does not
exist.
Either point of view, mixture or
solution, may be taken in describing solubility. The two points of view find
their expression in the reference states used for definition of activities,
activity coefficients and osmotic coefficients. Note that the composition of a
saturated mixture (or solution) can be described in terms of any suitable set of
thermodynamic components.
1.5.2.
Physicochemical Quantities and Units
Solubilities of solids have been
the subject of research for a long time, and have been expressed in a great many
ways, as described below. In each case, specification of the temperature and
either partial or total pressure of the saturating gaseous component is
necessary. The nomenclature and units follow, where possible.3 A few quantities follow
the ISO standards8 or
the German standard9;
see a review by Cvitaš10 for details.
A note on nomenclature
The nomenclature of the IUPAC Green Book3 calls the solute
component B and the solvent component A. In compilations and evaluations, the
first-named component (component 1) is the solute, and the second (component 2
for a two-component system) is the solvent. The reader should bear these
distinctions in nomenclature in mind when comparing equations given here with
those in the Green Book.
1. Mole fraction of
substance 1, x1 or x(1) (condensed phases),
y1 (gases):
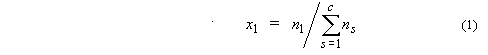
where ns is the
amount of substance of s, and c is the number of distinct
substances present (often the number of thermodynamic components in the system).
Mole percent of substance 1 is 100x1.
2. Ionic mole fractions of
salt i, xi+,
xi–: For a mixture of s binary salts i, each
of which ionizes completely into ns+ cations and nus–
anions, with nus = nus+ +
nus– and a mixture of p non-electrolytes j, of
which some may be solvent components, a generalization of the definition in11 gives:
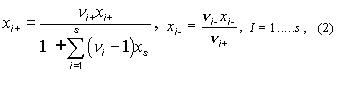
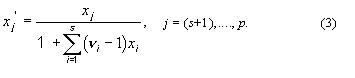
The sum of these mole fractions is unity, so that, with c = s + p,
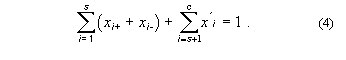
General conversions to other units in multicomponent systems are complicated. For a three-component
system containing non-electrolyte 1, electrolyte 2 and solvent 3.
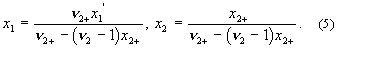
These relations are used in solubility equations for salts, and for tabulation of salt effects on
solubilities of gases (see below).
3. Mass fraction of substance 1, w1 or w(1):
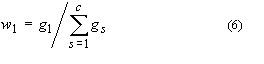
where gs is the
mass of substance s. Mass percent of substance 1 is 100
w1. The equivalent terms weight fraction, weight
percent and g (1)/100g solution are no longer used.
4. Molality of solute 1
in a solvent 2, m1:
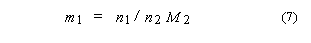
SI base units: mol
kg–1. Here, M2 is the molar mass of the solvent.
5. Aquamolality,
Solvomolality of substance 1 in a mixed solvent with components 2, 312,
m1(3):
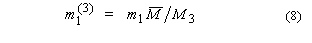
SI base units: mol
kg–1. Here, the average molar mass of the solvent is
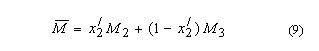
and x2' is
the solvent mole fraction of component 2. This term is used most frequently in
discussing comparative solubilities in water (component 2) and heavy water
(component 3) and in their mixtures.
6. Amount
concentration of solute 1 in a solution of volume V,
c1:
c1 = [formula of solute] =
n1/V ( 10 )
SI base units: mol
m–3. The symbol c1 is preferred to [formula of solute],
but both are used. The old terms molarity, molar and moles per unit volume are
no longer used.
7. Mole ratio,
rA,B (dimensionless)10
rA,B = n1 /
n2. ( 11 )
Mass ratio,
ZA,B, may be defined analogously10.
Mole and mass fractions
are appropriate to either the mixture or the solution point of view. The other
quantities are appropriate to the solution point of view only. Conversions
between pairs of these quantities can be carried out using the equations given
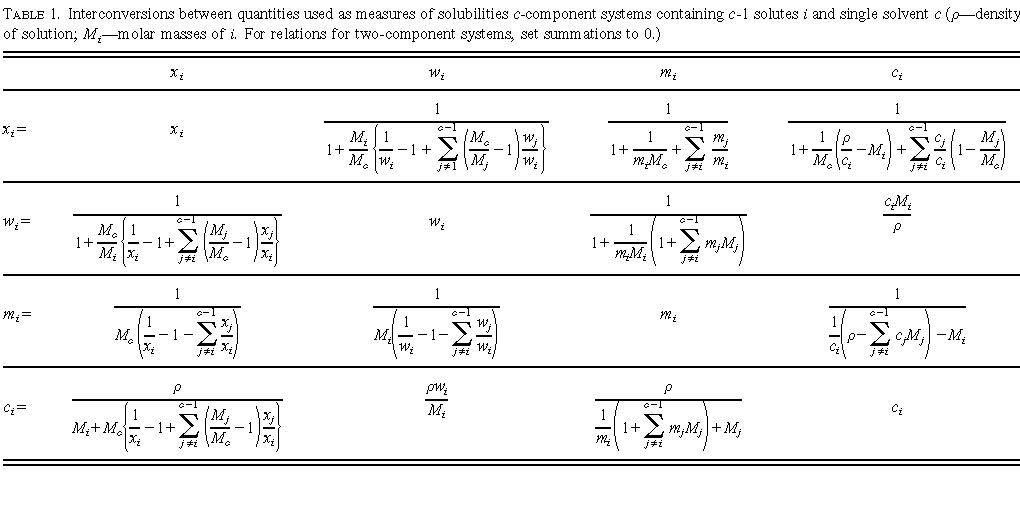
in Table 1 at the end of this Introduction. Other useful quantities will be
defined in the prefaces to individual volumes or on specific data sheets.
8. Mass
concentration of solute 1 in a solution of volume V, p1: SI
base units: kg m–3.
ρ1 =
g1/V (12)
9. Ionic strength,
Im (molality basis), or Ic (concentration basis):
Im = ½ Σi mizi2
Ic = ½ Σi cizi2 (13)
where zi is the charge number of ion i. While these quantities are not used generally to express solubilities, they are use to express the compositions of non-saturating components. For a single salt I with ions of charges z+, z-,
Im = |z+z-|vmi
Ic = |z+z-|vci (14)
Mole and mass fractions are appropriate to either the mixture or the solution point of view. the other quantities are appropriate to the solution point of view only. Conversions between some pairs of these quantities can be carried out using the equations given in Table 1 at the end of this Introduction. Other useful quantities will be defined in the prefaces to individual volumes or on specific data sheets.
In addition to these well defined SI-based units, other units have been used to express the solubilities of gases. Units and nomenclature follow, as modified by IUPAC recommendations. The equations describing Bunsen, Kuenen, Ostwald and absorption coefficients, as well as Henry's law constants, hold for ideal gases and perfect solutions only. Corrections of non-ideality should be made where possible. The corrections are less than 1 % for most gases near atmospheric pressure.
In much published data, the reference pressure is 1 atm = 0.101325 MPa rather than 1 bar = 0.1 MPa.
10. Bunsen coefficient,
α (dimensionless):
The volume of saturating gas, V1, reduced to T ° = 273.15 K, p° = 1 bar, which is absorbed by unit volume V2* of pure solvent at the temperature of measurement and partial pressure p° = 1 bar. If the gas is ideal, Henry's law (see below) holds, and the liquid is incompressible, then
α = (V °1/V*2) = (V1/V*2) (T °/T) (15)
11. Kuenen coefficient, S :
The volume of saturating gas, V(g), reduced to T ° = 273.15 K, p° = 1 bar, which is dissolved by unit mass of pure solvent at the temperature of measurement and partial pressure 1 bar. Thus,
S = V1T °/g2T = αVm,2/M2 (16)
SI base units: m3 kg-1. Here, M2 is the molar mass of the solvent. The Kuenen coefficient is proportional to the molality of the dissolved gas.
12. Ostwald coefficient, L (dimensionless) :
The volume of saturating gas, V1, absorbed by a volume V2* of pure solvent at the temperature and pressure of the measurement. Thus,
L = (V1/V*2) = (αT / T °) (p°/ p) (17)
The Ostwald coefficient is equal to the ratio of the amount concentrations in the gas and in the liquid.
13. Absorption coefficient, β (dimensionless):
The most common of several definitions of absorption coefficient is the volume of gas, reduced to T ° = 273.15 , p° = 1 bar absorbed per unit volume of pure solvent at a total pressure of 1 bar. The absorption and Bunsen coefficients are therefore very similar, and are connected by
β = α (1 - p2/p°) (18)
14. Henry's Law constant, KH:
KH = limx→0 (p1/x1) (19)
SI base units: Pa. Unfortunately, the definition is used often at finite mole fraction, even though this is a limiting law. The following have also been defined at Henry's Law constants:
K2 = p 1 / c1
Kc = c1g/ c1 (20)
where superscript g refers to the gas phase. K2 has SI base units Pa m3 mol-1, and Kc is dimensionless. The Henry's Law constant has also been called the Henry coefficient. Henry's Law can be used, with great caution, to convert data from the experimental pressure to 1 bar if the mole fraction of the gas in the liquid is small, and the difference in pressures is small.
The relations between the mole fraction solubility and the various quantities given above are as follows. Note again that these relations hold for ideal gaseous and perfect solution phases only.
x1 = 1 / [ 1 + ( RT ° / p°1V*m,2 α)] = 1 / [1 + ( RT °/ p°1M2S)]
= 1 / [ 1 + ( RT / p1V*m,2 L)] = 1 / [1 + ( RT °/ p°V*m,2β)] (21)
15. Salt effects on the Solubility of Gases
These are often reported as Sechenov (Setchenow, Setschenow) salt effect parameters y which are defined in various ways. The general semi-empirical Sechenov equation is
log(z1° / z1) = ksyz y (22)
where solubility is expressed in quantities
z, with superscript o designating pure solvent, and salt composition is expressed in quantities y. The quantities
c2,
m2,
x'2,
Im, and
Ic are used for
y, and quantities
c1,
m1,
x1+, α,
S and
L for
z, giving 30 definitions of
ksyz. Here, components 1 and 2 are the gaseous solute and electrolyte, respectively. The ratios of
z-values are the same for
z =
c1, α, and
L and for
m1 and
S, leaving 15 distinct definitions. If
z is the same, the definitions of
ksyz are related simply through 10 equations between pairs of
c2,
m2,
x'2,
Im, and
Ic. Some relations among the definitions, in terms of
kscc,
ksmm,
ksxx, are:
kscc = kscα =
kscL =
(m2 / c2) ksmc =
(x'2 / c2) ksxc =
(Ic / c2) ksIcc
ksmm =
(x'2 / m2) ksxm = ksmS =
(c2 / m2) kscm =
(Im / m2) ksImm (23)
ksxx =
(c2 / x'2) kscx =
(m2 / x'2) ksmx =
(Im / x'2) ksImx =
(Ic / x'2) ksIcx
These relations hold when a single salt is present; note that the relations between ionic strength and either molality or concentration are simple. If more than one salt is present, the ionic strength is the only practical quantity to be used for y.
Conversions between pairs of kscc, ksmm, ksxx are more complicated, and can be found using Eqn [5] and Table 1 at the end of the Introduction. For example,
ksxx = ƒ(m) [(ksmm /ν
2+) + (1 /m2) log ( ƒ(m) / ƒ(m°))] (24)
where
ƒ(m) = 1 + (m1 + ν2m2)M3
ƒ(m)° = 1 + (m °1m °2)M3 (25)
Errors in the salt effect parameters, as defined above, can be large. If the relative standard deviation in measurement of solubility is s(c1) / c1, the relative standard deviation in kscc is
s(kscc) / kscc= (√2 / c2kscc ln 10) (s(c1) / c1) (26)
For example, for kscc = 0.1 and c2 = 0.01 mol dm-3, s(kscc) / kscc is 30 % when s(c1) / c1 = 0.05 % and 1200 % when s(c1) / c1 = 2 %. At c2 = 1 mol dm-3, the corresponding errors are 0.3 % and 12 %, respectively.
If the solubility of a gas is greater than about x = 0.01 at partial pressure 1 bar, then several other factors must be taken into account, such as the density of the solution or the partial molar volume of the dissolved gas. In addition, corrections should be made for non-ideality of the gas.
In addition, the following definitions concerning density are useful in conversions between concentrations and other quantities.
16. Density (gas),
ρ, or γ:
ρ =g/V (27)
SI base units: kg
m–3. Here g is the total mass of the system.
17. Relative
density, d = ρ/ρ°: the ratio of the density of a mixture at
temperature t, pressure p to the density of a reference substance
at temperature t ', pressure p'. For liquid solutions, the
reference substance is often water at 4 °C, 1 bar. (In some cases 1 atm is used
instead of 1 bar.) The term specific gravity is no longer used.
Thermodynamics of
Solubility Thermodynamic analysis of solubility phenomena provides a
rational basis for the construction of functions to represent solubility data,
and thus aids in evaluation, and sometimes enables thermodynamic quantities to
be extracted. Both these are often difficult to achieve because of a lack of
experimental or theoretical activity coefficients. Where thermodynamic
quantities can be found, they are not evaluated critically, since this task
would involve examination of a large body of data that is not directly relevant
to solubility. Where possible, procedures for evaluation are based on
established thermodynamic methods. Specific procedures used in a particular
volume will be described in the Preface to that volume.
Only one thermodynamic result is mentioned here: the temperature dependence of solubility. Sometimes it is possible to fit the mole fraction solubility at various temperatures using the equation
ln x1 = A + B(T/K) + Cln(T/K) + D2(T/K) (28)
where A, B, C and D are constants to be determined from least-squares fitting of the data. Sometimes, to avoid singular matrices of the least-squares normal equations, T is scaled; e.g., T is replaced by T/100.
If the gas and the solution of the dissolved gas are ideal, the coefficients can be used to find standard thermodynamic functions for transfer of the gas from the vapor to the liquid phase at the standard pressure (1 bar) and infinitely-dilute dissolved gas, as follows.
ΔG°m,1 / R = - A - B - C(T/K)ln(T/K) - D(T/K)2 (29)
ΔS°m,1 / R = A + Cln(T/K) + C + 2D(T/K) (30)
ΔH°m,1 / R = - B + C(T/K) + D(T/K)2 (31)
ΔC°mp / R = C + 2D(T/K) (32)
Alternatively (but equivalently), the standard state of infinitely-dilute dissolved gas can be described as a hypothetical ideal gas at mole fraction x1 = 1, p = 1 bar.
1.6. References for the Introduction
1E. A. Hill, J. Am. Chem. Soc. 22, 478 (1990).
2IUPAC Commission
on Atomic Weights and Isotopic Abundances. Pure Appl. Chem. 63, 975
(1989).*
3I. Mills et al., eds. Quantities, Units and
Symbols in Physical Chemistry (The Green Book) (Blackwell Scientific
Publications. Oxford, UK, 1993).
4H. H. Ku, ,
p. 73; C. Eisenhart, p. 69; in H. H. Ku, ed., Precision Measurement and
Calibration. NBS Special Publication 300, Vol. 1. (Washington, 1969).
5J. Regaudy, S. P. Klesney, Nomenclature of Organic
Chemistry (IUPAC), (The Blue Book) (Pergamon, Oxford, 1979).
6V. Gold et al., eds. Compendium of Chemical
Technology (The Gold Book) (Blackwell Scientific Publications. Oxford, UK,
1987).
7H. Freiser, G. H. Nancollas, eds.
Compendium of Analytical Nomenclature (The Orange Book) (Blackwell
Scientific Publications, Oxford, UK, 1987). Sect. 9.1.8.
8ISO Standards Handbook, Quantities and Units
(International Standards Organization, Geneva, 1993).
9
German Standard, DIN 1310, Zusammungsetzung von
Mischphasen (Beuth Verlag, Berlin, 1984).
10T. Cvitaš, Chem. International 17, No. 4,
123 (1995).
11R. A. Robinson, R. H. Stokes,
Electrolyte Solutions, 2nd ed. (Butterworths, London, 1959).
12J. W. Lorimer, in R. Cohen-Adad, J. W. Lorimer,
Alkali Metal and Ammonium Chlorides in Water and Heavy Water (Binary
Systems), IUPAC Solubility Data Series, Vol. 47. (Pergamon Press, Oxford,
UK, 1991). p. 495.
This section was written
by:
A. F. M. Barton, Perth, WA, Australia; F. W. Getzen, Raleigh, NC, USA; G.
T. Hefter, Perth, WA, Australia; D. G. Shaw, Fairbanks, AK, USA
December, 1995
* There is now a
2001 update, IUPAC Commission on Atomic Weights and Isotopic Abundances. Pure
Appl. Chem. 75, 1107 (2003).